Spiral Chess
This modest variant is based on the single idea of a spiral mover. This is a (multiply) bent slider that moves along a trajectory that wraps around it like a spiral. An example of such a trajectory is shown below:
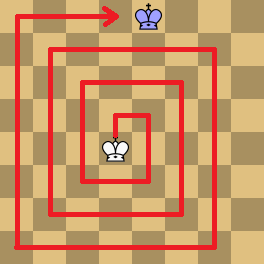
This move can be classified as oblique, meaning there are 8 symmetry-equivalent realizations of it. If we indicate this type of move in Betza notation as X, the depicted trajectory corresponds to rfX: starting in the forward direction as a W step, and then turning right.
A well-centered X mover can reach every square of an empty board even through one of its 8 moves. But it is very easily blocked, and even on an empty board loses many of its moves when it stands closer to a board edge. On an edge square it has the same destinations as an orthodox King, and the diagonal 'steps' can be blocked. (But you would have to occupy two squares orthogonally adjacent to the piece to do that.)
Setup
The start position is that of orthodox Chess, except that the King is replaced by a Spiral King.
Pieces
All pieces other than the royal move as in orthodox Chess. The Spiral King is a fully symmetric spiral mover. (I.e., it can start stepping in any of the 4 orthogonal directions, and from each continue clockwise or anti-clockwise.) In addition it can castle according to orthodox rules.
Rules
All rules of orthodox Chess apply. In particular, moves that expose the Spiral King to capture, or keep it exposed to capture are not legal.
Note, however, that the spiral move is not reversible. As a result, it is possible for one Spiral King to attack another, without being attacked back. Hence checkmates are possible even in the King-vs-King end-game.
Notes
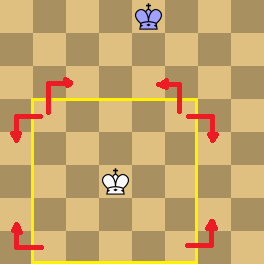
A useful way to envision the possible moves of a spiral mover is to consider the largest square-shaped empty area around it. Any square in this area can be reached. The outer-most pieces on each edge of the border surrounding this empty areas (excluding corners) will be under attack, but (if an edge contains multiple pieces) any squares between the pieces will be inaccessible. This because the spiral trajectories enter the border at the squares next to the corners, and move inward from there. Corners of the border are only reachable when one of the adjacent edges is entirely empty.

The spiral move was inspired by one of the crooked Nightriders in Jörg Knappen's variant Nachtmahr, (the 'diagonal wide' one), which had a trajectory that was so much folded that it had to pass through many squares to reach a relatively near destination. This set me thinking about the longest possible slider trajectory on a given board.
 This 'user submitted' page is a collaboration between the posting user and the Chess Variant Pages. Registered contributors to the Chess Variant Pages have the ability to post their own works, subject to review and editing by the Chess Variant Pages Editorial Staff.
This 'user submitted' page is a collaboration between the posting user and the Chess Variant Pages. Registered contributors to the Chess Variant Pages have the ability to post their own works, subject to review and editing by the Chess Variant Pages Editorial Staff.
By H. G. Muller.
Last revised by H. G. Muller.
Web page created: 2021-05-22. Web page last updated: 2021-06-06