Ubi-ubi chess
Ubi-ubi chess is an experimental chess variant, that came up in a discussion between Koen Versmissen and Dirk Borst at the house of Hans Bodlaender in January 1998.The Ubi-ubi is a rather strong fairy chess piece, and we wondered how this piece would do in a chess variant. The first variant tried was dismissed as `not good' after a little experimentation - a correction was not tried anymore. I'm told that ubi-ubi means `everywhere' in Latin.
First variant
The game is played with a standard chess set, with in the setup the pawns on the d-column and f-column are advanced one square, and the knights are considered to be ubi-ubi's.
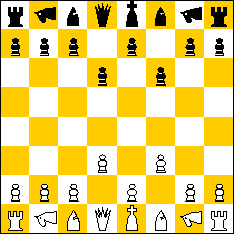 White:
White:
King e1; Queen d1; Rook a1, h1; Ubi-ubi b1, g1; Bishop c1, f1; Pawn a2,
b2, c2, d3, e2, f3, g2, h2.
Black:
King e8; Queen d8; Rook a8, h8; Ubi-ubi b8, g8; Bishop c8, f8; Pawn a7,
b7, c7, d6, e7, f6, g7, h7.
Ubi-ubi's can make arbitrary (but not infinitely) many knight moves, but must stop their movement when they take a piece from the opponent.
Comments
Dirk Borst (white) played against Koen Versmissen the following short game: 1. Qd2, Qd7. 2. Qg5, Qc6. 3. Qh5+, resign.Unfortunately, the game is flawed: after a little experimentation, it seems that the best white can do is to exchange all four ubi-ubi's, after which he has a better position in an otherwise further normal game of chess. If white does not exchange ubi-ubi's, then black should do so, while playing h3 is deadly for white.
Second variant
In the second (untried) variant, each player has only one ubi-ubi, but the player does not need to specify which of the two knights is an ubi-ubi. Only when a player makes a move with a knight/ubi-ubi piece that is not a normal knight move, then this determines which of the two is the ubi-ubi, and which is the knight. The game is again played from the same setup as the first variant.Now exchanging knights/ubi-ubi's would be disadvantageous, as the player whose piece is taken would determine the other `knight' to be the ubi-ubi.
Written by Hans Bodlaender.
WWW page created: February 20, 1998.
