Claustrophobia
This is an entry in the 45/46 cell 2007 design contest.Claustrophobia is played on a 5x8 board with 3 additional squares on each side - a total of 46 squares. These three squares constitute the palace, which initially holds the King, the Queen-Guard, and a Knight.
There is no castling for the king is already at a wing (in the palace), and the objective of the game is not just checkmate (which wins as usual), but to invade the palace of the opposing king with your king and capture the scepter. The scepter is located on the 3 squares of the palace, and can only be captured by the opposing king. The scepter must be protected at all cost for losing it forfeits the throne, power …everything.
Setup
Pieces
An 8x8 chess board and standard chessmen can be used to represent the new pieces as follows: Queen for Queen-guard, rooks for flying bombers, bishops for ninja guards.The Ninja Guard’s Moves
The Ninja Guard is a color bound piece that can move one or two steps diagonally. It can leap over a diagonally adjacent friendly piece to land exactly 2 squares away (a two-space diagonal leap). It can capture on any square it lands, and additionally it can can capture an enemy piece that is diagonally adjacent by jumping over it. It can capture two pieces (the first immediately adjacent to it, and the next right after) in its path on a diagonal by jumping over the first one and capturing the second piece on the square it lands. |
The Ninja Guard on c4 can capture all the pieces in the diagram.
It can capture the pawn on a6 by jumping over the knight at b5. It can capture the pawn on b3 by moving to b3 or by jumping over the pawn and landing on a2. It can capture the knight on d5 by moving to d5 or it can capture both the knight and the pawn by jumping over to e6. |
The Flying Bomber’s Moves
Standard Move:- The flying bomber eliminates an enemy piece by flying over it, and landing on the empty square immediately after it on the same orthogonal line. It cannot fly over or capture a second piece nor move beyond the first empty square after the enemy piece.
- The flying bomber can fly along any amount of empty squares (1-9) orthogonally, but not over any friendly pieces. This is identical to the movement of a rook.
Alternative Move: the Helicopter Landing
The Flying Bomber's peculiar short-range prowess is explained below:
- The Flying Bomber can fly over one friendly piece adjacent to it (left, right, up or down) and land on an empty square immediately after it. When it flies over a friendly piece adjacent to it, its range is limited to two squares.
- If an enemy piece is exactly 2 squares away orthogonally and no other piece is in-between, then the flying bomber can capture the usual way by flying over it and landing on any empty square after it. It can also capture by landing on the same square as the enemy like a Helicopter.
- If two enemy pieces lie on the same line,the first one adjacent to the bomber, and the next two squares away, then the flying bomber can eliminate both pieces by landing on the square of the second enemy piece. It cannot fly over the second enemy piece.
- Similarly, if there was a friendly piece in immediate vicinity of the bomber, and an enemy piece right after it, the Flying Bomber can fly over the friendly piece and destroy the piece right after by landing on the same square. Here too it cannot fly over beyond the enemy piece as it cannot fly over two pieces.
- The Flying Bomber needs at least one square to fly over for a bombing. e.g. it can destroy any enemy piece in its vicinity (1 square to left, right, up or down) by flying over it and landing on any empty square after it, but if a friendly piece occupies a square immediately after the enemy piece, no capture can be made.
For diagrams illustrating the moves see Flying Bombers Grand Chess
*note that the limited version of the flying bomber is used for this game - fly over and land on the empty square immediately after the enemy piece.
The Extra-mobile sliding pawn
The pawn moves and captures exactly as in orthodox chess except for the following. Normally, when a pawn faces an opposing pawn or an enemy piece, the pawn is blocked. However, the sliding pawn can, under these circumstances only if it is blocked, slide pass the enemy piece or pawn with the same 1-step diagonal movement that it would make when capturing.The Queen Guard
The Queen Guard moves exactly like the King, 1 step orthogonally or diagonally. Ironically, the Queen-Guard despite appearing to be less powerful than the flying bomber, can deliver mate with the help of a king.Moves over unused squares
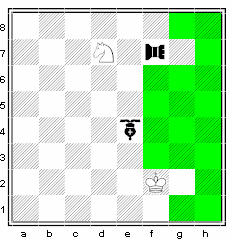 |
The flying bomber at f7 is checking the king at f2 because it can capture by going to f1.
Note that the unused squares do not hinder the movement of any pieces. The Ninja Guard on e4 is attacking the square g2 and so the king cannot go there. The flying bomber is threatening the knight on d7 as well. It can fly over, bomb the knight and land on c7. It can also eliminate the knight by going to d7 since it is exactly 2 squares away. |
Rules
The rules are as in orthodox chess except as noted below:- There is no castling as the king is already in its palace where it is normally safe.
- In addition to checkmate, a side can also win by capturing the opposing king's scepter.
Black's scepter is in the palace on f8,f7,or g7 and white's scepter on f1,f2,or g2.
Only the king can capture a scepter, so for example,if the white king marches towards the black king's palace, black can use this opportunity to checkmate, or drive the white king away and march the black king towards the opposing palace. - Pawns promote on the last rank to Queen-guard, ninja-guard,flying bomber or knight.
- The unused squares do not hinder the movement of any pieces.
- All rules governing draws including stalemate are exactly as in orthodox chess
Notes
- The flying bomber and a king cannot pry out an opposing king from its palace nor deliver mate.
- A lone ninja guard and a king can pry the opposing king out if, for white if the ninja guard is colorbound to black (same color as the extreme edge square g7 of black king's palace) or for black the ninja guard is color bound to white (correspond to g2).
- A knight cannot deliver mate but can succeed with the help of the king and with a timely sacrifice divert the opposing king away from the palace.
- A Queen-Guard with the help of a king can mate but cannot always pry the opposing king out of the palace.
- If ahead in pawns, it is best to try to exchange off the flying bombers since they can be a nuisance in the endgame.
 This 'user submitted' page is a collaboration between the posting user and the Chess Variant Pages. Registered contributors to the Chess Variant Pages have the ability to post their own works, subject to review and editing by the Chess Variant Pages Editorial Staff.
This 'user submitted' page is a collaboration between the posting user and the Chess Variant Pages. Registered contributors to the Chess Variant Pages have the ability to post their own works, subject to review and editing by the Chess Variant Pages Editorial Staff.
By Charles Daniel.
Last revised by H. G. Muller.
Web page created: 2007-09-17. Web page last updated: 2022-12-05