Caïssa
Caïssa is a chess variant, invented by Christian Freeling in 1982. Christian regards this as one of his most interesting chess variants, and wrote me (in Dutch) that the game has a unique method of taking, and removes more prejudices about chesssystems than any other.The description below is taken from the website of Christian Freeling and Ed van Zon (with permission) (slightly edited by me); and also the pictures were taken from this website, called Mindsports.
See the Mindsports website for more information on Christian Freeling's other chess variants, methods to play several of these on the Internet against others, and more. There also is a variant on a board make of hexagons: HexCaïssa.
Rules
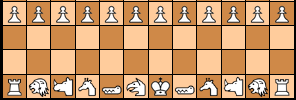
Caïssa is played with two players on a board of size seven by seven.
 White:
White:
Queen c2; Rook c3; Knight b2; Bishop d2.
Black:
Queen e6; Rook e5; Knight f6; Bishop d6.
The diagram shows the Caïssa board with the pieces in the initial position. Initially, the board is covered with 49 tiles.
All play is on the tiles. White begins. Players move, and must move, in turn.
The connection rule
The tile-complex must remain 'connected', that is, a tile or group of tiles must always remain orthogonally or diagonally connected to the rest.The queen
The King's role is played by the Queen. The diagram below shows its options for movement and capture in a non-check situation. The Queen is the only piece with the power of capture in the usual sense.

If in check, the Queen is restricted to the King's move, as shown in the diagram below. Thus a Rook or Bishop giving check from a distance, need no cover!

If the Queen moves, the tile it vacates is removed in the same turn. The removal is compulsory, but it may not violate the connection rule.
The check rule
Queens that see one another along the same rank, file or diagonal, are considered to be 'mutually in check'. It follows that neither player may effectuate this situation. Thus a Queen may protect a piece against capture by it's counterpart.The pieces
The pieces move as in Chess. Under the implicit condition of not putting its own Queen in check and the explicit condition of not violating the connection rule, a piece can always move to any of its target-squares, whether or not it is tiled, and if it is, whether or not it is occupied, and if it is, regardless of the colour of the occupying piece.If the target-square has no tile, the piece takes its own tile with it. At the end of the move the tile-complex must still be connected.
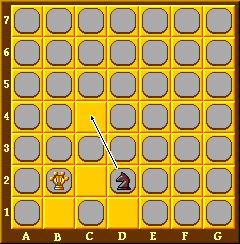
There is no 'during the move', so the Knight in the next diagram may legally move to the square marked A. Moving to B is of course illegal.

The mate in 1 in the next diagram shows another application of tile-surfing and the connection rule.
If the target-square is occupied by a friendly piece, the player must exchange the pieces.
If the target-square is occupied by an opponent's piece, the player must also exchange the pieces, but there is one exception: a switch between two pieces of the same type may not in the next turn be 'undone' by the opponent.
This, then, is Caïssa's unique way of mutual capture between pieces, capture by exchange, which is in fact no capture at all. The necessity of the last rule should be obvious. It represents a situation similar to the one that gave birth to the 'ko' rule in the game of Go.
Comment
Pritchard gives on details different rules in his Encyclopedia of Chess Variants: especially, the first player may arrange an initial position in which no queen is in check, and the second player chooses the site to play. He also writes:Some beautiful combinations are possible and no draw has so far been recorded.
Rules written by Christian Freeling for the Mindsports Website, slightly edited for the Chess Variant Pages, and introduction and comments added by Hans Bodlaender. Rules and images copyright Mindsports; used here with permission.
WWW page made: November 3, 1997. Last modified: January 23, 2005.