Interdependent Chess

Introduction

Interdependent Chess is a Shogi-style variant in which Chess pieces can capture only with the assistance of a neighboring piece. Basically, a piece can capture with the capturing power of any neighboring piece it moves directly away from. The one exception to this is the Universalist, which has no native powers of movement or capture. It is the one completely interdependent piece. It can move only as a neighboring piece, and instead of granting its own powers of capture, it lets the piece use its own powers. On it's own, the Universalist is completely powerless, but with another Universalist, it becomes the most powerful piece on the board.

Interdependent Chess was invented by Fergus Duniho in November 2001 for the 42 squares contest. It began with inspiration from Ralph Betza's Worse than Worthless article on pieces with negative value. I initially set out to create a game in which every piece had negative value. Paradoxically, the pieces ended up giving each other value in an interdependent manner. This led to the name of Interdependent Chess. As I continued playtesting and changing the game, I focused more on the idea of interdependent pieces than on negative value pieces. With some guidance from Robert Abbot's article on What's Wrong With Ultima, Negative 42, as I initially called it, evolved into the game described here.

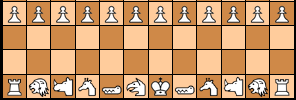
Setup

Black King (k): d7 Universalist (u): c7 Spider (s): a7, f7 Knight (n): b7, e7 Conservative (c): a6, f6 Guardian (g): b6, e6 Steward (t): c6, d6 White King (K): d1 Universalist (U): c1 Spider (S): a1, f1 Knight (B): b1, e1 Conservative (C): a2, f2 Guardian (G): b2, e2 Steward (T): c2, d2

+---+---+---+---+---+---+ 7 |:s:| n |:u:| k |:n:| s | +---+---+---+---+---+---+ 6 | c |:g:| t |:t:| g |:c:| +---+---+---+---+---+---+ 5 |:::| |:::| |:::| | +---+---+---+---+---+---+ 4 | |:::| |:::| |:::| +---+---+---+---+---+---+ 3 |:::| |:::| |:::| | +---+---+---+---+---+---+ 2 | C |:G:| T |:T:| G |:C:| +---+---+---+---+---+---+ 1 |:S:| N |:U:| K |:N:| S | +---+---+---+---+---+---+ a b c d e f

Short Rules

Detailed rules will follow the piece descriptions, but it will help to get an overview of the rules before reading the piece descriptions. The rules, as described in this section, are complete and accurate, though some details may go unexplained. The detailed rules are provided merely to better clarify and explain how to play the game.

Aside from differences in board, pieces, and setup, which are described above and below, Interdependent Chess is played like FIDE Chess with the following exceptions:

1. Captured pieces change sides and are held in hand by the capturing player, who may use a later turn to drop a captured piece on an empty space.
2. To capture, a piece must move directly away from another piece, which is toroidally adjacent to it.
1. If it moves directly away from a Universalist, it captures with its own powers of capture.
2. If it moves away from another piece, it captures with the capturing power of the piece it moves away from.
3. If one Universalist moves away from another, it can move or capture as a Bishop on a torus. This is the only move that can travel across the board as a torus. All other moves are limited by the edges of the board.
3. The Universalist is the only piece that also borrows the non-capturing moving power of a toroidally adjacent piece. It makes a non-capturing move by moving directly away from a piece with any non-capturing power of movement available to that piece. For most pieces, capturing and non-capturing powers are identical, but they are not identical for divergent pieces.
4. An isolated Universalist cannot move.
5. There is no castling, no promotion, no double moves, and no en passant capture.

Pieces

	The King moves as the King in FIDE Chess, except that it never has any opportunity to castle. It moves one space in any direction, but may not move into check.
	The Universalist is what Anthony Dickins calls a supernumerary piece. It isn't based on other pieces and was created especially for this game. A Universalist moves or captures as a neighboring piece by moving directly away from it. With respect to divergent pieces, whose moving or capturing powers are different, a Universalist can make a non-capturing move as the piece would, and it can capture as the piece would, but it cannot make a non-capturing move as the piece captures, and it cannot capture as the piece moves without capturing. In Interdependent Chess, this specifically applies to moving away from the Steward or Guardian. An isolated Universalist cannot move at all. When one Universalist moves directly away from another, it moves as a Bishop on a torus.
	The Knight moves as a Knight in FIDE Chess. For the purposes of this game, it is understood to travel along a two-step path to its destination. This can be one orthogonal step, followed by one diagonally outward step, or one one diagonal step, followed by an orthogonally outward step. When a piece moves away from a Knight, it can capture on the two spaces a Knight could reach with a path that begins with a step directly away from the Knight. A Universalist can also move to these two spaces without capturing.
	The Spider leaps two spaces orthogonally or diagonally. It is a compound piece that moves as an Alfil (Elephant) or Dabbabah (War Machine).
	The Conservative moves along its rank as a Rook in Chess, sliding any number of spaces horizontally. It is called a Conservative, because it won't move forward on its own. In a less interdependent variant, this would be an extremely weak piece, because it could never move off its starting rank. And that may be why I've never seen it in any variant. But in this game, it can move forward with the help of other pieces, and a captured Conservative can be dropped on any rank. This makes it more valuable than it would initially seem.
	The Steward is an omni-directional Pawn. It is borrowed from John William Brown's Centennial Chess. It can move one space orthogonally (as a Wazir) without capturing, and its capturing move is one space diagonally (as a Ferz). When a piece is toroidally and diagonally adjacent to it, that piece may capture one space diagonally by moving directly away from it. When it moves directly away from a toroidally adjacent Universalist, it can capture as a Ferz, though not as a Wazir. When a Universalist moves directly away from a toroidally adjacent Steward, it must capture if it moves away from it diagonally, and it must not capture if it moves away from it orthogonally. In this game, the Steward gets no double move and may not capture by en passant.
	The Guardian is an omni-directional Berolina Pawn. I invented it as the Berolina counterpart of the Steward. It can move one space diagonally (as a Ferz) without capturing, and its capturing move is one space orthogonally (as a Wazir). When a piece is toroidally and orthogonally adjacent to it, that piece may capture one space orthogonally by moving directly away from it. When it moves directly away from a toroidally adjacent Universalist, it can capture as a Wazir, though not as a Ferz. When a Universalist moves directly away from a toroidally adjacent Guardian, it must capture if it moves away orthogonally, and it must not capture if it moves away diagonally. In this game, the Guardian gets no double move and may not capture by en passant, though it should be able to in larger games.

Detailed Rules

Interdependent Chess is played like FIDE Chess, except that it has a different set of pieces, a different board, different rules regarding capture, and no Pawns, no castling, and no promotion. The board and pieces are shown and described above. The most important difference from FIDE Chess is how capturing happens.

First of all, when a piece is captured, it changes color, and the capturing player gets to hold it in hand until he chooses to drop it back on the board. When a player chooses, he may use his turn to drop a piece in hand onto an empty space. There are no restrictions on which empty space a piece can be dropped except that it shouldn't leave or put one's own King in check. This is all familiar stuff from Shogi, which is why I'm getting it out of the way first. What really distinguishes this game is not what happens when you capture; it is how you capture.

To capture a piece, a piece must borrow the capturing ability of a neighboring piece. It does this by moving directly away from the piece. For every piece but the Steward and Guardian, this is best shown with diagrams for how the Universalist moves. The Universalist can move only as a neighboring piece. With respect to non-divergent pieces, the Universalist borrows the same powers of movement for non-capturing moves as another piece does when it captures.

The first three show it moving as a Spider by moving away from one. The fourth diagram shows it moving as a Conservative by moving away from a Conservative. The fifth one shows a Universalist moving away from a King by moving away from one.

Here are some diagrams of moving away from a Knight:

The Knight is understood as moving one orthogonally, then one diagonally outward, or one diagonally, followed by one orthogonally outward. When a Universalist moves away from a Knight, it goes to the two spaces that can be reached by a Knight path that begins with a step directly away from the Knight. In the first diagram, the first step is orthogonal, and the second step is diagonal. In the second diagram, the first step is diagonal, and the second is orthogonal. Other pieces borrow the capturing power of the Knight in the same way.

When a piece moves away from a Steward or Guardian, it can capture only as the piece captures, which is diagonally for the Steward and orthogonally for the Guardian. If it's a Universalist, it can make a non-capturing move away only by using the piece's non-capturing powers of movement, which is orthogonal for a Steward and diagonal for a Guardian. Here are some diagrams to illustrate this:

The first diagram shows a Universalist that can move diagonally away from an adjacent Guardian or orthogonally away from an adjacent Steward. The second diagram shows the same pieces in the same positions, and it adds a second Steward and Guardian to the spaces the Universalist could move to in the first diagram. If Stewards and Guardians captured as they move, the Universalist would be able to capture the pieces on the squares it could move to previously. But it cannot, because it is not in a position to use the capturing moves of the Steward and Guardian on its right. But it is in a position to use the capturing powers of the two on its left, and these allow it to capture either of the two on its right. Notice that it is now the Steward that gives it a diagonal move, and it is the Guardian that gives it an orthogonal move. This is the reverse of what it was in the first diagram.

When a piece is on the edge or in a corner, it can move away from a piece on another part of the board as though the board were an anchor-ring or torus board. This is a board that is cylindrical both horizontally and vertically. Its left and right sides are connected, and its far and near sides are connected. Here is one way to understand this. A torus is the shape of a doughnut. Take the board in your imagination and fold it into a cylinder whose left and right sides touch. Then fold it again so that the top and bottom sides touch. It is now torus shaped, the shape of a doughnut.

In his Guide to Fairy Chess, Anthony Dickens suggests something like this for visualizing an anchor-ring board, as he calls it:

Imagine that the middle board is the one you're playing on. This diagram shows how spaces on opposite edges of an anchor-ring or torus board are connected to each other. Since the board has an odd number of ranks, the diagonals on the near and far ranks do not connect with matching color diagonals. Since this can make things very confusing, I have made the board out of color gradients, creating the optical illusion that near and far edge diagonals do match each other in color. For example, a7 and f1 look like they're on the same diagonal, because they are both light-squared spaces at opposite corners. But it is an optical illusion. Although they are diagonally connected on a torus, they belong to different diagonals on the main board.

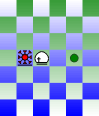
The PBM version does it differently. Instead of using an optical illusion, it displays toroidally adjacent spaces next to each other. This screenshot from the PBM gives you a visual representation of adjacency on a torus. In this image, the f file is copied on the left of the a file; the a file is copied on the right of the f file; rank 1 is copied above rank 7; and rank 7 is copied below rank 1.

With one exception, to be described later, pieces do not move on the board as though it were a torus. Their movement is bounded by the boundaries of the board. But for the purposes of granting capturing and moving abilities to adjacent pieces, adjacency is conceived of as adjacency on a torus. Here are some diagrams that illustrate this:

In the first diagram, the Universalist at f4 is toroidally adjacent to the Knight at a4, giving it the power to move away from a4 as a Knight. In the second diagram, the Universalist at f4 is toroidally adjacent to the Conservative at a4, giving it the power to slide left as a Conservative. Note that the Universalist can even capture the Conservative, because the Conservative's move is long-ranged enough to reach the other side. The third diagram shows a Universalist that is toroidally adjacent to a Knight at a7 and a Spider at f7. It can move away from the Knight to d2 and e3, and it can move away from the Spider to f3.

Finally, there is one piece that can move on the board as though it were a torus. This is the Universalist when it is moving away from another Universalist. When one Universalist moves away from another, it moves as a Bishop on a torus. Due to the geometry of a 6x7 anchor-ring board, this move can cover every square on the board when it is unobstructed. To help you visualize this move, here is a series of diagrams, progressively increasing the distance of obstruction. These diagrams should help you visualize the path that a Universalist takes in moving diagonally around the whole board. The piece used in the diagram is a Bishop, because I made the diagrams before I removed that piece from the game, and they remain as they are, because the actual piece used isn't relevant to what the diagrams show.

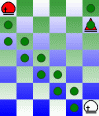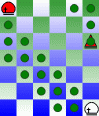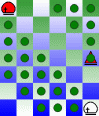Computer Play

I developed this game using Zillions of Games, and most of my diagrams are screenshots from the Zillions implementation. You can download this here:

Download interdependent.zip

You can also play Interdependent Chess by online correspondence, using the web-based Game Courier system on this site.