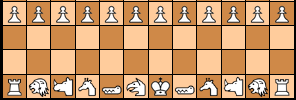
Checkmating Applet (3 vs 1)
This page allows you to practice your technique for checkmating a bare King. Just move a piece of the side you want to play with, and the computer will reply with the best move for the other player.
This applet is exclusively for 3-vs-1 end-games, and has some limitations: it assumes none of the pieces would be able to inflict checkmate with only the help of its King, not even help mates. So it will only consider ways of winning that preserve all its pieces, even when sacrificing a piece could lead to a faster mate. For practicing 2-vs-1 end-games, go here.
At the bottom of this page there is a general explanation of the theory of checkmating with two minors.
|
graphicsDir=/membergraphics/MSelven-chess/
whitePrefix=w
blackPrefix=b
graphicsType=png
squareSize=35
useMarkers=1
enableAI=0
symmetry=none
promoZone=0
maxPromote=0
Fairy piece:X:N:marshall:a1
Fairy piece:Y:N:archbishop:b3
King::K:king:b2,,d4
|
Generating end-game table; Please wait. |
||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
Building EGT... This can take a minute.Design your own pieceIn the pane below you can define moves of a piece by clicking the squares it should be allowed to move to. First click defines a leaper move to the square. A second click would convert this to a slider/rider move that repeats that step/leap. A third click would remove the move again. To limit the range of a slider you can click the first square along its path that it should not be able to reach. Clicking on the piece takes away all its moves, and thus clears the entire pane. After you are satisfied with the move, you can assign it to one of the pieces through the buttons on the right. Note that you can specify divergent pieces by changing the move before you press the button a second time; normally you would just press it twice, though.
|
|||||||||||||||||||||||||||||
Checkmating with pairs
To be able to checkmate with orthodox Kings and a single piece on a rectangular board, that piece would have to cover two orthogonally adjacent squares. When none of your pieces does that (as this applet assumes), your best hope is to force checkmate with two pieces. We will see that some minor pieces are better at this than others. We can distinguish several mating patterns:

Corner mate:
1.Na3+ Ka1 2.Bc3#
Pieces that can do this (such as the Bishop, or Modern Elephant (FA)) can be called 'potent'. They are very useful for checkmating, and can force mate together with almost any partner, if they are not both excessively weak (or color-bounds on the same shade). Often having 8 moves between the two of them is already enough.

Edge mate:
1... Ka1 2.Cb4+ Kb1 3.Nc3#
Edge mates - We will call a piece 'forking' if it can attack two squares separated by two orthogonal steps simultaneously. A Knight is an example of this. (But, as we shall see, an unlucky example.) Together with a piece that can attack the square in between, it would be able to deliver checkmate along a board edge. E.g. the forking piece can attack a1 and c1, while its King at b3 keeps the bare King trapped against the edge. It must launch the attack when the bare King is on a1. When the forking piece is not also a piece that can deliver a corner mate (c1-a1 switch), the other piece must have been forcing the bare King into the corner by zugzwang, covering c1. That other piece must then switch its attack from c1 to b1 to deliver the edge mate.
Again this requires a 3-move (uncapture + move + capture) tour, but now to travel from c1 to b1, instead of a1. Pieces with this ability can be called 'semi-potent'. These cannot force mate with just any partner, though; only together with a forking piece. We could say forking and the c1-b1 switch are each half the key to the problem, while a c1-a1 switch is a full solution on its own.
The Knight can actually do both: fork a1 and c1, and move from c1 to b1 in 3 moves. So why do two Knights fail to force checkmate? Turns out that to fork a1 and c1, the Knight must be on b3, where its King also has to be to cover a2, b2 and c2. Having the King on a3 is no good for an edge mate, unless the piece that delivers the check on b1 also happens to attack c2 on the side. Again, in theory the Knight could do that, from a3. But again that is exactly where the King has to be! A Wazir on c1 does attack both b1 and c2, though, and can also make the 3-move tour from c1 to b1. So Knight plus Wazir can deliver checkmate.
Color binding, orientation and board size - The properties (semi-)potent and forking are defined with respect to a corner. For color-bound pieces this means they could have the property in some corners, but not in others, with as a consequence that mate is only possible in corners of a certain shade. Since on odd-sized boards all corners have the same shade, this would mean forcing checkmate is only possible when the color-bound piece is on one shade, and not when it is on the other.
Of course with two color-bound pieces it is also essential that they are not on the same shade, as the other shade then is a safe haven for the bare King. Even if there is only one corner that none of your (non-royal) pieces can reach, it would not be possible to smoke out the bare King once it takes shelter there, and we would have a fortress draw. (As is well known from the end-game Rook-Pawn plus wrong Bishop in orthodox Chess.) If you can cut off the King from such a safe corner it might still be possible to force checkmate in one of the others. Such end-games are neither generally won nor generally drawn, but have a win percentage somewhere in between.
When the checkmate can only be performed in some of the corners, this has an impact on the required board size. Most piece combinations involving leapers lose their ability to force checkmate at some point when the board size is increased. (For non-square boards it is usually the smallest dimension that counts.) Simply running away from the opponent's pieces proves an effective defense, as the strong player cannot keep up with all his pieces, (even chasing just with his King will consume most of his turns), and the pieces that can keep up might not have the power to confine or slow down the escaping King enough for the remaining pieces to catch up. When mate cannot be forced in all corners, this makes the board effectively look larger. So it can happen that a piece combination involving a color-bound piece is too weak to force checkmate on 8x8, but has no trouble to do that on 9x9, provided the color-bound piece is on the required shade (e.g. with Ferz plus Wazir).
Semi-potent pieces are by definition not color-bound, but could suffer other forms of area binding (e.g. to ranks) if they are asymmetric. Even without area binding asymmetric pieces could have the forking or (semi-)potent property only along some of the edges, but fortunately edges in two directions are present near each corner. The complementary properties forking and semi-potence should be along the same edge to be of use, though; a vCvW is forking along a rank, and semi-potent along a file, which is not a viable combination, and a pair of them cannot force checkmate. Rotate one of those by 90 degrees (sCsW), and together they can.
With only two-fold symmetry it can happen that a piece only has a property along one of the edges. (E.g. a Crab is only forking along the furthest rank, as is a fFbsN, which can actually force mate together with a Wazir on 8x8.) Checkmates dependent on that property can then only be performed in the two corners at the end of that edge.

Double edge mate: 1.Zd4#
Double edged - A rarer pattern occurs with a Ferz, a forking piece that can fork both edges at once: with this you can trap a King on two diagonally adjacent squares near the corner, say b1 and a2. Just put the Ferz on b2, protected by a King on c3. If you now have a piece that attacks diagonally adjacent squares, such as a Zebra, you can deliver mate with it by attacking b1 and a2 simultaneously. And again, a Knight does make such an attack, but only from c3, where the King must be to protect the Ferz without attacking a2 or b1. (Fortunately for Knight and Ferz they can do an edge mate, where the Ferz is the forking piece on b2, and the Knight switches attack from c1 to b1 (e.g. moving from e2 to c3) to deliver mate.) These mates work only in the corner of the shade of the Ferz, and together Z+F or N+F are too weak to drive the bare King from the safe corner to the deadly one on 8x8, so it still is a general draw. But on 9x9 with the Ferz on the corner shade both are a general win.
The two edge squares next to the corner are of the same shade, and can thus also be simultanously attacked by color-bound pieces like Kirin (FD) and its stronger cousin FAD. (But not the Modern Elephant (FA), which does attack diagonally adjacent squares, but only in a radial pattern for which there is no room in a corner.) Because of their D move these pieces are potent, but because of their color binding ony in corners of their own shade. In the other corners, in combination with a Ferz on the other shade (or each other, as they also have F moves), they can deliver the double-edge mate.
Choice mates - Some strong compound leapers, such as a Marquis (WN) or an FAD can attack (say) b1, d1 and a2 simultaneously, while the King is on c3. (Which again disqualifies the Knight, which could only make these attacks from c3.) This creates two 'eyes' (a1 and c1) that a second piece only would have to attack to checkmate a King there. There might be no need then to drive the King into the corner by checking it on b1 by guarding c1 in advance; if you have another forking piece that can attack a1 and c1 simultaneously (e.g. a Ferz moving to b2), moving to c1 won't bring solace for the bare King. Even when your other piece isn't forking, you could have a piece that can choose whether it will attack a1 or c1; these are of the same shade, so even color bounds and color alternators often are able to do that. The condition is that you should be able to make the tour between these square in four moves. (Or, more precisely: a move, a capture, a retro-move and a retro-capture.)
 This 'user submitted' page is a collaboration between the posting user and the Chess Variant Pages. Registered contributors to the Chess Variant Pages have the ability to post their own works, subject to review and editing by the Chess Variant Pages Editorial Staff.
This 'user submitted' page is a collaboration between the posting user and the Chess Variant Pages. Registered contributors to the Chess Variant Pages have the ability to post their own works, subject to review and editing by the Chess Variant Pages Editorial Staff.
By H. G. Muller.
Last revised by H. G. Muller.
Web page created: 2020-06-23. Web page last updated: 2020-06-23